谷歌大模型获重大突破，首次拿下国际奥数银牌

专注AIGC领域的专业社区，关注微软&OpenAI、百度文心一言、讯飞星火等大语言模型（LLM）的发展和应用落地，聚焦LLM的市场研究和AIGC开发者生态，欢迎关注！

谷歌DeepMind公布了一项重大成绩，使用AlphaProof和AlphaGeometry 2两个混合大模型参加了2024年国际数学奥林匹克竞赛（IMO）并获得了银牌。

IMO是最古老、权威的数学竞赛，每年都会有来自世界各地精英级数学家参与，同时也是AI模型的竞技场，是衡量其数学推理能力的最佳平台。

在今年的比赛中，一共有6道数学题，每答对一道获7分。AlphaProof解决了两道代数和一个数论问题；AlphaGeometry 2答对了一道几何题，一共获得了28分仅比金牌少1分。

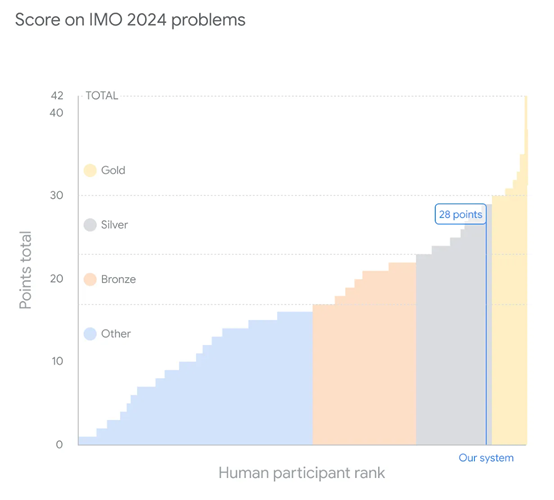
值得一提的是，AlphaProof解答了今年IMO比赛最难的一道题，609位参赛者只有5个人给出了正确答案。

AlphaGeometry 2

早在今年1月17日谷歌便发布了AlphaGeometry模型，并在30道几何奥林匹克测试题中答对了25道，这比之前由中国著名数学家、计算机家-吴文俊提出的最先进方法还多15道，仅比人类金牌得主少0.9分。

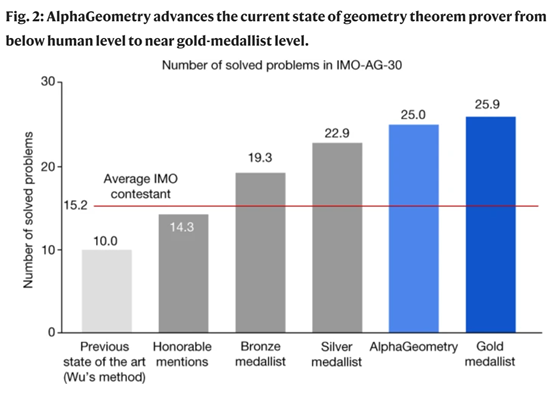
AlphaGeometry的核心在于其神经符号框架，一个能够自动解决欧几里得平面几何问题的复杂模型，绕过了传统机器学习方法中对大量人类证明数据的依赖，实现了从零开始的自我学习，使得AlphaGeometry能够生成大量的合成定理和证明，构建出一个有向无环图，表示所有可达到的结论。

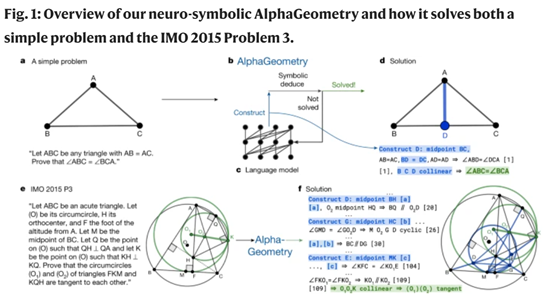
证明搜索是AlphaGeometry神经符号框架的核心之一，这是一个循环过程，语言模型和符号推理引擎交替运行。

语言模型根据问题陈述生成新的辅助构造，符号推理引擎则利用这些构造扩展其推理闭包，直到达到结论或达到最大迭代次数。在每一次循环中，语言模型都会根据当前的证明状态和已有的构造生成一个新的辅助构造。

然后，符号推理引擎会将这个新构造纳入考虑，尝试通过逻辑推理来接近或达到结论。如果推理引擎能够证明定理，搜索过程结束；如果不行，循环将继续，语言模型将生成另一个辅助构造。

证明修剪是AlphaGeometry另外一个重要功能。在自动证明过程中，可能会生成一些不必要的辅助构造，这些构造虽然不是错误的，但它们可能会使证明过程变得冗长和复杂。通过证明修剪可以去除这些不必要的构造，确保证明的简洁性和可读性。

AlphaGeometry通过穷举试验和错误的方法进行证明修剪。模型会尝试丢弃每个辅助点的子集，并重新运行符号推理引擎，以验证在没有这些辅助点的情况下是否仍然能够达到结论。通过这种方式，模型能够找到并返回所有可能证明中的最短路径。

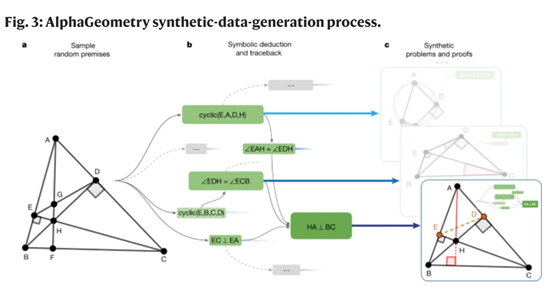
此外，在合成证明生成中，AlphaGeometry引入了“依赖差异”的概念，这一概念允许系统生成构建辅助点的证明步骤，并超越了纯符号推理的范围。

辅助构造是几何证明中的一个关键挑战，它代表了证明过程中的无限分支因素。通过这种方式，AlphaGeometry能够生成几乎无限的证明变体，为深度学习模型提供了丰富的训练数据。

而AlphaGeometry 2是在一代的基础之上进行了大量迭代和技术创新，使用了谷歌自研的Gemini作为语言模型，并在比一代多一个数量级的合成数据上从头开始训练。

AlphaGeometry 2使用的符号引擎比其前身快两个数量级。当出现新问题时，使用一种新的知识共享机制来实现不同搜索树的高级组合，以解决更复杂的数学难题。

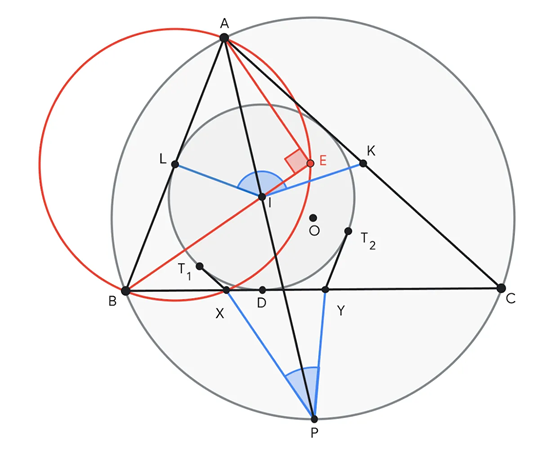
在今年IMO比赛之前，AlphaGeometry 2可以解决过去25年所有IMO几何问题的83%，而一代解决率只有53%。

在今年正式比赛中，AlphaGeometry 2在收到几何问题后，仅用19秒便解决了这道难题，达到了人类难以企及的超高效率。

AlphaProof

AlphaProof是谷歌最新开发的一个专门用于形式数学推理的模型，其核心特点是结合了预训练语言模型和AlphaZero强化学习算法，能够在复杂的数学问题上展现出强大的推理能力。

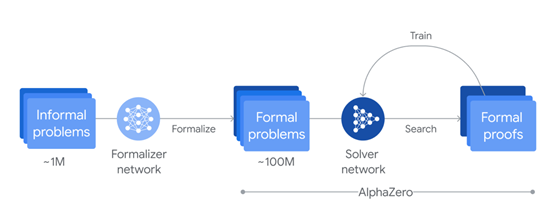
AlphaProof的工作原理是使用形式语言Lean来进行数学证明。形式语言的优势在于可以严格验证推理步骤的正确性，但传统上受限于人工编写的数据量较少。

为了解决这一难题，AlphaProof使用了一个经过微调的Gemini大模型，将自然语言问题自动转换为形式语言表述，从而创建了一个包含各种难度和数学主题的大规模形式问题库。

在面对一个新问题时，AlphaProof会生成解决方案候选，然后通过在Lean中搜索可能的证明步骤来证明或反驳这些候选解。每个被发现和验证的证明都会用来强化AlphaProof的语言模型，提高它解决后续更具挑战性问题的能力。

为了备战2024年IMO，AlphaProof在比赛前的几周内进行了密集数据训练，证明或反驳了数百万个问题，涵盖了广泛的难度和数学主题领域。

谷歌表示，目前的AI模型在解决一般的数学问题时仍然存在困难，主要是因为推理的局限性和训练数据不足。本次参数的两个混合大模型已经具备数学推理的AGI（通用人工智能）能力，可以帮助数学专家发现新的解题方法，同时也是AI在数学领域的重大技术突破。

本文素材来源谷歌官网、论文，如有侵权请联系删除

END

本篇文章来源于微信公众号: AIGC开放社区